!!!!!!!!!!!!!!!!!!! Piotr:

	|1−x|
Dana jest funkcja y=		podaj zbiór wartości i przedziały monotoniczności
	x2−1

Lidka: wydaje mi się,że zbiorem wartości funkcji sa liczby nalezace do zbioru<0;nieskończoności) ale tio tak na 90 procent

Lidka: to*

Piotr: a jak to liczyłaś niby?

Lidka: patrzysz na mianownik −xnigdy nie bedzie mniejsze od zera bo x² daje Ci zawsze liczbe dodatnia,a w liczniku tez bedzie dodatnie bo masz wartosc bezwzgledna. takie sa moje przypuszczenia,ale tak jak napisalam,nie jestem pewna,wiec lepiej zeby ktos na to jeszcze zerknal.

asdf: a dziedzina to gdzie ?

Piotr: a jak w tym przypadku wyliczyć dziedzinę?

asdf: x² − 1 ≠ 0 x = −1 lub x = 1 D = R \ {−1;1}

ABC: mianownik nie moze byc rowny zero.piszesz ze x² −1 nie jest rowne 0 i liczysz. wyjdzie ze x² = 1 ,ale tez wiesz,ze −1 ! d=R−{1}−{−1}

Piotr: to ten zbiór wartości powyżej wyliczony jest dobry, bo mi się wydaje, że nie

asdf: mi ZWF wyszedł: (−∞;−1) v (1;∞) sprawdzi to ktoś?

Piotr: proszę

Piotr: a jak to wyliczałeś?

asdf: sorry, według mnie zwf to od (0; ∞) albo od (0,1>, które prawidłowe?, a dziedzine to nie wiem po co liczyłem, bo trzeba podać zbiór wartości funkcji

asdf: @Piotr, masz geogebre? to narysuj punkty: f(1) = 0 f(2) = 1/3 f(3) = 2/8 f(4) = 3/15 f(5) = 4/24 f(−1) = 0 f(−2) = 3/3 f(−3) = 4/8 f(−4) = 5/15 f(−5) = 6/35 Tu można zauważyć, że największą wartością będzie argument −2

Piotr:

	1
a ja w podr. mam taką odp. (−∞,−		)u(0,∞) i nie wiem skąd to się wzięło a za przedziały
	2

nie wiem też jak się zabrać

asdf: to ja nie rozumiem

Piotr: no ja właśnie tego też nie rozumiem

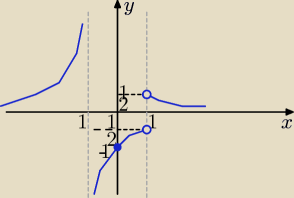
Eta: D=R\{−1,1}

	x−1		1
1o dla x >1 f(x)=		=
	(x−1)(x+1)		x+1

	−(x−1)		−1
2o dla x<1 i x≠ −1 f(x)=		=
	(x−1)(x+1)		x+1

	1
1o f(1)=
	2

	1
2o f(1)= −
	2

	1
ZW= (−∞, −		) U ( 0,∞)
	2

f(x) ↗ x∊ ............. f(x)↘ x€ ........

Piotr: dziękuję